To the theory of the Pliocene – Pleistocene and Holocene climate

ВВЕДЕНИЕ

Понять генезис происходивших в прошлом изменений климата трудно по ряду причин. Во-первых, это связано с недостаточностью информации. Восстановление палеоклимата основано на интерпретации и абсолютном датировании косвенных показателей, что сопряжено с определенными погрешностями. Реконструкции всегда отражают динамику климата определенного региона, причем типично, когда данные разных регионов недостаточно хорошо коррелированы между собой. Поэтому составление из мозаики региональных шкал (да еще очень разреженной) картины планетарных изменений (требуемой для теоретического анализа) осуществляется с определенным произволом. Эта задача решается различными способами, от самого простого усреднения информации до развития палеореанализов (Franke et al., 2017; Anderson et al., 2019), которые в настоящее время охватывают только небольшие отрезки прошлого. Разумеется, последний способ обеспечивает пространственно-временное распределение климатических переменных любого пространственного разрешения (в рамках использованной модели атмосферы), однако вопрос качества полученных полей остается. И вообще при такой процедуре верификация результатов становится затруднительна, поскольку модель (с заданными внешними форсингами) “подтягивается” под данные реконструкций климата.

Во-вторых, существует естественное ограничение интервала времени истории Земли, для которого создается теория. Это связано с тем, что на разных временных масштабах факторы климатообразования различны. Поэтому, если, например, предполагается (как в данной статье) анализ изменений климата при приблизительно одинаковом распределении материков и океанов, то уходить далеко в прошлое не следует. В этом случае разумно ограничиться последними ~5 млн л., используя для анализа соответствующие реконструкции (например, Zachos et al., 2001).

В-третьих, климатологи убеждены в определенных позициях, способствующих пониманию механизмов климатообразования, однако эти представления неполны. Ясно, что климатические изменения происходят в энергетически открытой воздействиям солнечной энергии Земной системе, динамику которой отражают “первые принципы”, т.е. законы сохранения момента количества движения масс воздуха и воды, энергии, массы воздуха, массы водяного пара, углерода и др. Принимается, что поступающая солнечная энергия варьирует из-за изменений светимости Солнца и вулканического аэрозоля в различных масштабах (более длительные вариации, чем столетние, просто неизвестны), а на тысячелетних интервалах – из-за изменений параметров орбиты Земли и наклонения ее оси вращения (в соответствии с теорией Миланковича). Однако кроме энергетики не исключены влияния других физических факторов. По-видимому, это касается неравномерности вращения Земли (Сидоренков, 2002), причем в контексте теории климата в этом направлении практически ничего не сделано. Возможно, в принципе, и обнаружение новых эффектов, предугадать которые мы не в силах именно потому, что не имеем о них никаких представлений. На то, что появление неожиданных эффектов возможно, указывает опыт развития климатологии: так, о климатической значимости событий Дансгора–Оешгера (DO) и Хайнриха (H) (Ou, 2022) стало известно сравнительно недавно (~20 л. н.).

Законы сохранения формулируются в форме уравнений, составляющих основу математических моделей Земной системы (полных моделей и моделей промежуточной сложности), решение которых может быть осуществлено только численными методами с помощью компьютерных расчетов. Моделирование палеоклиматов интенсивно развивается последние 30 лет в рамках последовательных (1–4) стадий проекта PMIP (Paleoclimate Modelling Intercomparison Project https://pmip.lsce.ipsl.fr ), причем в последние ~15 лет PMIP стал работать по протоколу и в рамках CMIP (Coupled Model Intercomparison Project https://www.wcrp-climate.org/wgcm-cmip ). В этих работах принимают участие десятки моделей климата из различных стран. Компьютерные эксперименты направлены на воспроизведение климата в “канонические” срезы палеовремени 21 и 6 тыс. л. н. (характеризующие максимум последнего оледенения и условия межледниковья). Кроме этого проводится моделирование климата предыдущего межледниковья (127 тыс. л. н.), воспроизводится динамика климата за последнюю тысячу лет (эксперимент “Millennium”) и выполняется тестовый эксперимент “Preindustrial”, воссоздающий доиндустриальный климат. Главная цель PMIP – валидация моделей, предназначенных для осуществления климатического прогноза, однако эти данные полезны и для развития теории климата, описывающей изменения природной среды в прошлом.

Обращаясь к этим результатам, следует иметь в виду то, что из-за исключительной сложности моделей данные моделирования часто не менее трудно интерпретировать, чем эмпирические сведения. В этом случае результаты сопоставляются с упрощенными схемами эволюции простых динамических систем, чтобы попытаться понять механизмы происходящих изменений, которые затем, как предполагается, можно перенести на сложные объекты. Однако при этом есть опасения (к сожалению, небезосновательные), что упрощенная картина при применении к сложной системе может дать принципиально неверные результаты.

Идеальная теория климата должна описывать как планетарные, так и региональные изменения. Попытка такого рода – воссоздать в детальном компьютерном моделировании изменения климата (вместе с динамикой всей природной среды) за последние 20 тыс. л. – была недавно предпринята в рамках проекта PalMod ( https://www.palmod.de/ ). Тенденции глобальных изменений получились правильные, но на региональном уровне палеотемпературы, палеогидрологический режим и другие характеристики не продемонстрировали хорошего количественного сходства с данными эмпирических реконструкций.

Поскольку детальные теоретические обобщения являются делом будущего, в данной работе делается попытка подвести своеобразный промежуточный итог – объяснить главные особенности динамики планетарного климата за последние ~5 млн лет. Картина складывается из следующих фрагментов. Это, во-первых, общее похолодание от плиоцена к плейстоцену и изменившаяся на этом фоне амплитуда и преобладающая ритмичность колебаний климата. Действительно, до ~1.5 млн л. н. климат Земли следовал 41-тысячелетним вариациям наклонения оси вращения планеты к плоскости орбиты (например, Venti et al., 2013). Также прослеживались циклы в 23 и 19 тыс. лет. Эти вариации имели (сравнительно с последующим периодом) сравнительно небольшую амплитуду, причем, в условиях повышенной фоновой температуры, не сопровождались активизацией ледниковых щитов. Чувствительным внутренним элементом, усваивающим сигналы изменяющейся инсоляции, были тропические муссоны (например, Lourens et al., 2010). Механизм заключался в том, что при их активизации в атмосфере выделялось большое количество скрытого тепла, и этот сигнал потепления транслировался атмосферными волнами всей климатической системе.

Данный режим (“Мир 41”, в терминологии, введенной на 5 конференции PAGES (5th PAGES Open Science Meeting, Сарагоса (Испания), 2017)), существовал длительное время на фоне постепенного снижения температуры, которое было генетически связано с генеральным снижением концентрации СО ₂ в воздухе. После перехода гляциологического порога ~2.5 млн л. н. (например, Tan et al., 2018), активизировались обратные связи термического режима с гляциосферой, что привело к появлению обширного ледникового щита Гренландии и периодическому развитию/разрушению других ледниковых щитов. Оледенение Северного полушария стало теперь тем чувствительным элементом климатической системы, к которому перешла функция управления глобальными климатическими изменениями. При этом перестроилась ритмичность (этот процесс занял около 0.5 млн л.) – вместо превалирования 41-тысячелетних колебаний доминировать стали ~100-тысячелетние колебания – “Мир 41” перешел в “Мир 100”. Более формальный взгляд на причины данной перестройки режима колебаний климатического режима дан в (Mukhin et al., 2019).

Важной особенностью указанных циклов является то, что их вклад в дисперсию не является основным. Главную роль играют случайные флуктуации (“шум”). Они характеризуются сплошной функцией спектральной плотности ( S , спектр), описывающей распределение дисперсии по частотам. При этом периодичности, указанные выше, проявляются на фоне шума. Форма спектров разная на межгодовом, “вековом” и тысячелетнем масштабах, что является интегральным показателем того, что механизм вариаций климата различен. Причем из континуума “вековых” флуктуаций выделяются события DO и H, механика которых представляется достаточно конкретизированной, а также те события, которым можно приписать генезис, связанный с воздействием форсингов за счет вариаций светимости Солнца, трендов парниковых газов и колебаний прозрачности атмосферы при крупных вулканических извержениях (Mann, 2011).

Претендующая на полноту теория призвана дать согласованное описание всех этих планетарных эффектов, раскрыть вызывающие их механизмы и служить основой для понимания механизмов проявления региональных изменений климата.

В данной работе предполагается объяснить природу названных эффектов, используя для этого данные реконструкций и моделирования, а также привлекая для анализа современные представления о динамике сложных систем. При обращении к данным реконструкций принимаются во внимание ограничения, связанные с точностью информации, однако какой-либо специальный анализ того, каким способом данные получены, какова их погрешность и др., проводиться не будет.

ВАРИАЦИИ ИНСООЛЯЦИИ И ОБРАТНЫЕ СВЯЗИ В КЛИМАТИЧЕСКОЙ СИСТЕМЕ

История крупных изменений климата, прослеживаемых десятки-сотни миллионов лет, была историей вариаций СО₂ (Будыко и др., 1985). Снижение температуры на протяжении последних нескольких десятков миллионов лет связано с масштабным уменьшением концентрации СО₂ в атмосфере.

Основой понимания природы регулярных климатических циклов (41 и ~20 тыс. л.) является теория Миланковича, в которой ищутся связи изменений климата с вариациями инсоляции на внешней границе атмосферы (ВГА) (Berger, 1978; Berger, Loutre, 1991). С точки зрения небесной механики, параметры, определяющие радиационный режим планеты, т.е. наклонение (угол между плоскостями экватора и эклиптики, ε), эксцентриситет ( e ) и долгота перигелия (максимально близкая к Солнцу позиция Земли относительно весеннего равноденствия, в угловых координатах, ) не константы, а сложно устроенные функции времени. Наклонение колеблется от 22° до 24.5° с периодом в 41 тыс. л. В современную эпоху ε = 23.44°. Позиция перигелия смещается относительно положения равноденствия с ритмичностью в 19 и 23 тыс. л. Эллиптичность орбиты варьирует (весьма слабо) с периодичностью, немного меньшей, чем 100 тыс. л.

Изменения радиационного режима управляются динамикой ε и $\varpi$ . В качестве иллюстрации часто используют кривую летней инсоляции на 65° с. ш., которая состоит из сложных нерегулярно повторяющихся положительных и отрицательных аномалий, сгенерированную калькулятором VSOP (Variations Séculaires des Orbites Planétaires) (Milankovitch cycles – Wikipedia, VSOP (planets) – Wikipedia). Эта широта показательна тем, что тут оба фактора вносят одинаковый вклад в вариации. Кроме того, кривая демонстрирует приход радиации к полярному кругу, т.е. к условной границе среднегодового распространения морских льдов и снежного покрова.

Анализ поведения реконструированного климата продемонстрировал те же периодичности: 41 и 19–23 тыс. л. Это дает основание серьезно отнестись к идеям о существовании связи вариаций инсоляции с колебаниями климата. Однако механизм этой связи далеко не тривиален: требуется понять, как могут сформироваться вариации климата при нулевых годовых аномалиях притока солнечной энергии, поскольку изменения параметров ε и $\varpi$ обеспечивают только перераспределение энергии по широтным зонам и сезонам, а значения эксцентриситета (и его изменения, которые влияют на годовую сумму радиации), очень малы.

Влияние вариаций ε можно интерпретировать, рассуждая, что важнее для потепления/похолодания климата: комбинация “положительная аномалия прихода радиации летом и отрицательная аномалия зимой”, или противоположная структура. Самим М. Миланковичем была априорно высказана идея, что изменения климата следуют за аномалиями инсоляции летнего Северного полушария, т.е. в симметричном сезонном радиационном влиянии приоритет принадлежит аномалиям теплого периода года.

Несимметричность отклика связана с обратными связями в климатической системе. Один из эффектов связан с тем, что аномалии парниковых свойств, управляемые содержанием водяного пара в воздухе, более эффективны при повышенном фоне температуры. Действительно, из-за экспоненциального характера зависимости насыщающего парциального давления водяного пара от температуры ($E=E\left(t\right)$), одна и та же аномалия температуры $\left(\pm ∆t\right)$ при фоновых высоких или низких температурах обеспечит существенно разные изменения $\left(\pm ∆t\right)$ . То есть изменение содержания водяного пара и аномалии парниковых свойств эффективнее в теплое время года.

Другой механизм обеспечивается за счет действия альбедной обратной связи, когда за счет увеличения (уменьшения) ε происходит рост (снижение) годового притока радиации в высокие широты – именно в тот регион, в котором формируется полярное оледенение. Это провоцирует уменьшение (увеличение) площади снега и льда и активирует развитие альбедной обратной связи, результатом действия которой являются нарастающие изменения климата определенного знака. В низких широтах инсоляция пропорционально уменьшается (растет), однако здесь нет криосферных элементов, способных интенсифицировать изменения климата.

Кроме того, при аномально повышенном облучении солнечной радиацией Северного полушария, как уже было отмечено, активизировались тропические муссоны, и дополнительно выделяющееся в атмосфере скрытое тепло шло на создание положительной аномалии температуры.

Рассмотренные обратные связи реализуются очень быстро – от дней до сезона. Более медленным регулятором изменений климата является положительная обратная связь между состоянием климата и углеродным циклом, в которой механизм влияния на температуру реализуется посредством усиления/ослабления парникового эффекта.

Так же, как изменения наклона, можно охарактеризовать влияние изменений долготы перигелия ($\varpi$). Например, в современном состоянии орбита такова, что перигелий приходится на зиму Северного полушария (а афелий на лето) и сезонные различия сглаживаются, а ~10 тыс. л. н. конфигурация была противоположной и за счет этого фактора различия были максимально обострены.

Приведенные связи вариаций инсоляции с колебаниями климата выглядят убедительно, но, на самом деле, они представлены совершенно умозрительно. Дело в том, что, оперируя только рассуждениями такого типа, можно получить и противоречивые результаты. Например, казалось бы, ясная идея ускоряющей изменения климата альбедной обратной связи может быть сведена на нет, если принять во внимание, что при развитии похолодания в полярной области увеличивается межширотный градиент температуры, что должно вызвать активизацию переноса тепла в высокие широты и ликвидацию похолодания.

Эта недоказуемость открывала широкие возможности спекуляций, и концепция неоднократно подвергалась сомнениям, отвергалась и переосмысливалась (также умозрительно). Необходимым средством, позволившим подтвердить правильность теории, послужило математическое моделирование климата, обеспечившее, по выражению А. Берже (Berger, 1978) “ренессанс теории Миланковича”.

МОДЕЛИРОВАНИЕ КЛИМАТА ЭПОХ МЕЖЛЕДНИКОВИЙ И ОЛЕДЕНЕНИЙ

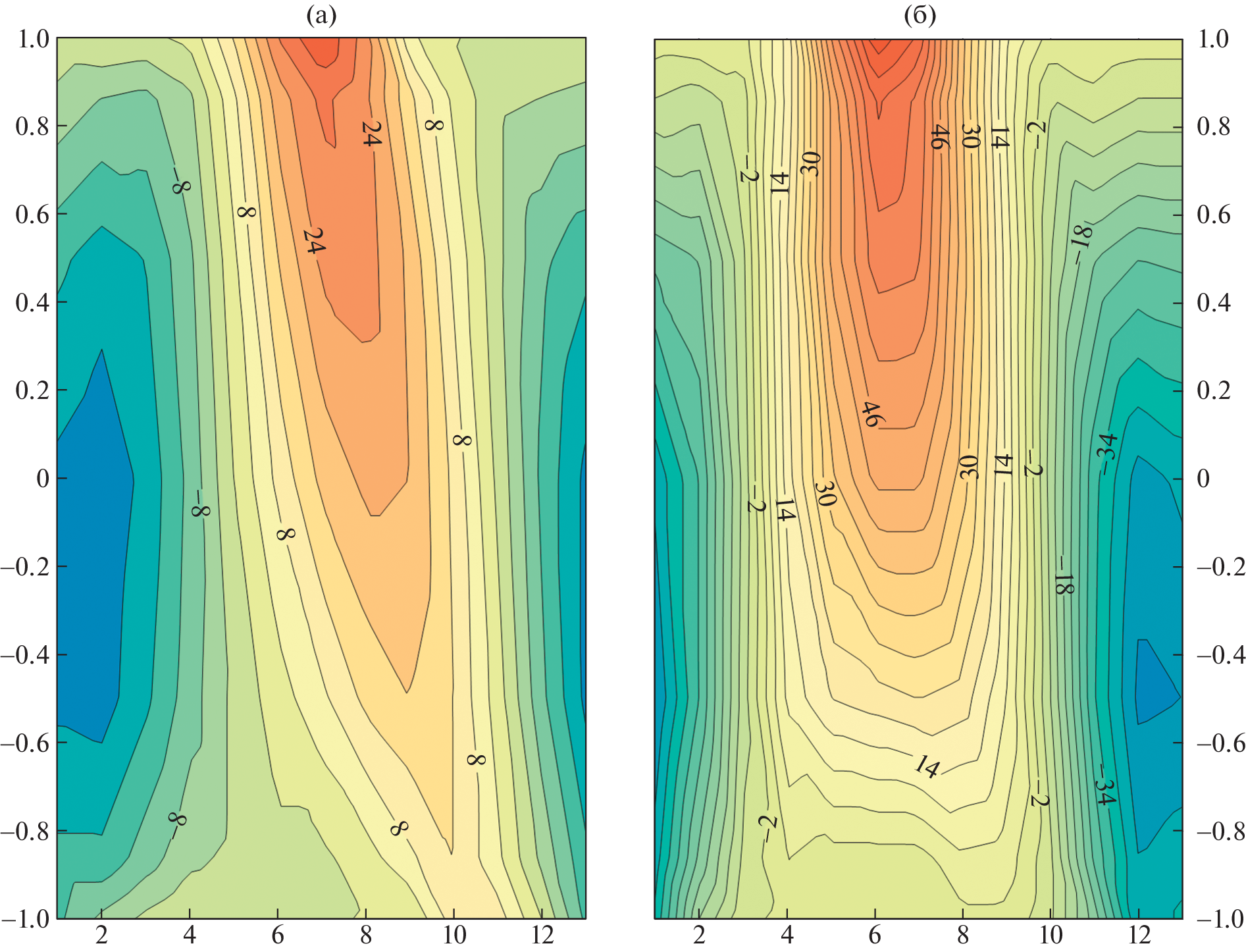
Сравним климат середины голоцена и современный климат. Отличия создали отклонения инсоляции на ВГА, определяемые увеличением наклонения (ε = 24.105), и изменение долготы перигелия ($\varpi$ = 180.87°: перигелий приходился на лето северного полушария, а афелий – на зиму), что усиливало летнюю положительную аномалию инсоляции и отрицательную аномалию зимой (рис. 1, (а)).

Рис. 1. Аномалии инсоляции на ВГА (Вт/м²) для 6 (а) и 127 (б) тыс л. н. На оси абсцисс – номера месяцев, на оси ординат – синус широты (Южное полушарие <0). Расчеты проведены на основе алгоритмов и программ, представленных в (Berger, 1978). Fig. 1. Insolation anomalies on the MAA (W/m2 ) for (a) 6 and (б) 127 kyr ago. On the abscissa axis, the numbers of the months, on the ordinate axis, the sine of latitude (Southern Hemisphere <0). The calculations were carried out on the basis of the algorithms and programs presented (Berger, 1978)

Аномалия инсоляции была максимальная ~9000 л. н. (рис. 2), однако для анализа был выбран срез времени 6000 л. н., что мотивировано тем, что к середине голоцена уже исчезли остатки Скандинавского и Лаврентийского ледниковых щитов, поэтому компьютерные численные эксперименты представляли собой в чистом виде реакцию климата на вариации инсоляции.

Рис. 2. Аномалии инсоляции на ВГА (Вт/м² ) за последние 21 тыс. л. (ось ординат; 0 – настоящее время). На оси абсцисс – номера месяцев. Расчеты проведены на основе алгоритмов и программ, представленных в (Berger, 1978). Fig. 2. Anomalies of insolation on the VGA (W/m2 ) for the last 21 thousand years (y-axis; 0 is the present time). On the abscissa axis are the numbers of the months. The calculations were carried out on the basis of the algorithms and programs presented in (Berger, 1978).

Модельные расчеты проводились неоднократно во всех четырех фазах PMIP (см. выше). В результате получены согласованные результаты, различия связаны с тем, что несколько разными задавались концентрации парниковых газов (Brierley et al., 2020). В умеренной зоне Северного полушария было воспроизведено заметное повышение температуры летом над континентами, и менее выраженное похолодание зимой, т.е. годовые аномалии получились положительными и гораздо лучше выраженными на материках. Температура морской поверхности и межширотный перенос тепла в океане не претерпели существенных изменений. В Южном полушарии аномалии инсоляции на ВГА сезонно зеркальны, поэтому положительная аномалия температуры отмечается в июне-августе и отрицательная в декабре-феврале. В середине голоцена отчетливо проявилась активизация (по сравнению с современной) муссонных циркуляций Африки и Южной Азии. Эти результаты правильно воспроизводят повышенную увлажненность Северной Африки в раннем и среднем голоцене, однако дают неполное представление о пространственной масштабности данного явления (Brierley et al., 2020).

Предыдущее межледниковье, ассоциируемое с морской изотопной стадией (МИС) 5е, максимально проявилось около 127 тыс. л. н. Аномалии инсоляции (рис. 1 , (б)), отвечающие параметрам планеты для данной эпохи (ε = 23.9°, $\varpi$ = 90°), получились более масштабными, чем те, что наблюдались в середине голоцена, поэтому и температура была несколько выше. Затем на протяжении ~10 тыс. л. глобальная температура понизилась на несколько градусов (стадия 5d). Моделирование показало, что этот переход управлялся изменениями инсоляции, отвечающими изменению параметров планеты. Так, 115 тыс. л. н. набор параметров был иным: ε = 22.4° и $\varpi$ = 270°.

Вновь получено убедительное свидетельство того, что муссоны интенсивнее в период максимума потепления и их активность убывает при переходе к холодной эпохе. Причем оказалось, что в зоне действия муссона Гвинейского залива (Западная Африка) темп изменений осадков (осредненных по территории муссонного региона), связанных с изменениями параметров ε и ϖ, во время обеих межледниковий практически одинаков (–0.07 мм/1000 лет). На Индостане темпы ослабления муссона в голоцене были в два раза меньше (–0.05 мм/1000 лет), чем в предыдущее межледниковье (–0.12 мм/1000 лет) (Braconnot et al., 2008). Это связано с неодинаковостью структуры аномалий инсоляции (см. рис. 1, (а), (б)) и различиями в реакции на этот фактор региональных муссонных систем.

Рассмотрим результаты моделирования климата позднеплейстоценового похолодания. При вычислениях задавалось распределение инсоляции для времени 21 тыс. л. н., которое было очень близким к современному (рис. 2). Климатические отличия получились благодаря тому, что в граничные условия введены дополнительные к существующим в настоящее время ледниковые щиты и снижена концентрация углекислого газа. В результате моделями PMIP воссозданы повсеместно на Земле отрицательные аномалии температуры, максимальные (до –20°С) в регионах, занятых Лаврентийским, Кордильерским, Скандинавским, Баренцево-Карским ледниками (Ka-geyama et al., 2021). При этом модельные температуры PMIP4 немного выше, чем в PMIP3, что связано (как и в случае моделирования условий голоцена – см. выше) с уточнением концентраций парниковых газов. Осадки практически повсеместно уменьшились (кроме тропической зоны южного полушария в Тихом океане), особенно велики изменения в регионах ледниковых щитов и во Внутритропической зоне конвергенции (достигающими 300–700 мм/год). Математическое моделирование продемонстрировало и изменения циркуляционных особенностей, в частности, сдвиг к югу оси струйного течения над Северной Америкой и частью Атлантики (Kageyama et al., 2021), а так же смещение к югу позиции полярного фронта (Beghin et al., 2015).

100-ТЫСЯЧЕЛЕТНИЙ ЦИКЛ В ИЗМЕНЕНИЯХ КЛИМАТА

При интерпретации механизма связи инсоляции и климата следует иметь в виду, что, несмотря на несомненное воздействие орбитальных факторов на формирование особенно выраженных похолоданий/потеплений, в среднем не более 20% дисперсии временных рядов может быть объяснено колебаниями в 41, 23 и 19 тыс. л. (Wunsch, 2003). Больший вклад в изменчивость вносят 100-тысячелетние ритмы и, интегрально, “шумовые” флуктуации, которым в теории Миланковича нет места. Поэтому требуются объяснения, выходящие за ее рамки.

Главным ритмом изменений климата плейстоцена является ~100-тысячелетний, отражающий переходы между ледниковым и межледниковым состоянием природной среды. Такое поведение можно интерпретировать с позиций перехода из одного состояния в другое за счет так называемого “переброса” (имитирующего случайно следующие друг за другом положительные и отрицательные аномалии), причем его преобладающий ритм (определяемый внутренними параметрами климатической системы) можно сделать близким к наблюдаемому (Kislov, 2009).

Этот механизм может быть дополнен учетом влияния колебаний эксцентриситета. Как было уже отмечено, они вызывают очень слабые, климатически незначимые вариации солнечной радиации. Однако, поскольку их периодичность близка к средней периодичности “переброса”, то эти первоначально малоамплитудные вариации могут усиливаться, “выращиваясь” за счет резонанса (так называемого стохастического резонанса).

Данная гипотеза получена в рамках очень простой модели, поэтому спорно переносить эти результаты на сложную Земную систему, хотя в некотором смысле определенное подтверждение есть в (Ganopolski, Calov, 2011). Можно с такой же степенью достоверности предложить и другие механизмы, приводящие к развитию 100-тысячелетнего колебания. Например, модель запаздывающего осциллятора (когда фазы колебаний температуры и оледенения сдвинуты на ~10 тыс. л. (Kislov, 2009)) и др. Более важно подчеркнуть то, что 100-тысячелетние колебания климата стимулированы максимумами инсоляции и активизированы внутренними процессами климатической системы.

Возможно, именно из-за сложности механизма, строгого соответствия между величинами максимумов и масштабностью теплых аномалий климата нет. Так, межледниковья, соответствующие морским изотопным стадиям (МИС) 5е, 7с, 15а, были, несомненно, реакцией на мощные аномалии инсоляции, однако не менее масштабные теплые события МИС 1, 9е, 15е и 17 возникали при сравнительно умеренных аномалиях, а события МИС 11с и 19с отвечали совсем слабому росту притока радиации. Иногда же, наоборот, в ответ на мощную аномалию инсоляции возникал слабый температурный отклик (МИС 9а). Это говорит о том, что для формирования теплого события аномалия инсоляции в Северном полушарии необходима, но ее присутствие не гарантирует развития межледниковья в полном объеме (Tzedakis et al., 2017).

В этом контексте получается, что орбитально-индуцированные вариации инсоляции важны не столько сами по себе, сколько как своеобразный “метроном” или “кардиостимулятор”, задающий ритм климатических изменений. Отметим, что именно так и была сформулирована роль астрономического фактора в одной из первых публикаций на данную тему (Hays et al., 1976).

СПЕКТРЫ КОЛЕБАНИЙ КЛИМАТА

Комплексной характеристикой временной динамики климатической системы служит ее функция спектральной плотности S, которая описывает распределение по частотам (периодам) “энергии” колебаний. Поскольку в качестве характеристики изменений климата применяется температура, то под энергией понимается дисперсия ее флуктуаций, величина, с размерностью К ².

В спектре вариаций инсоляции энергия сосредоточена только вблизи максимумов, соответствующих циклам Миланковича (Huybers, Curry, 2006). Спектр вариаций климата совершенно другой – он сплошной, т.е. вклад в дисперсию вносит каждая периодичность. Преобладающей является низкочастотная изменчивость, выражаемая зависимостью

$S=a{f}^{-k}$, (1)

где f – частота, $k>0$. В логарифмических координатах формула (1) выражена прямой линией с наклоном, равным (рис. 3). Объяснить сплошной характер спектра, т.е. присутствие в вариациях колебаний со всеми частотами, можно только если предположить, что энергия, попадающая в климатическую систему в определенном частотном диапазоне, перетекает в другие масштабы, т.е. образуется так называемый каскад энергии.

Рис. 3. Спектры флуктуаций температуры в разных диапазонах изменчивости. S – функция спектральной плотности (в относительных единицах, в логарифмическом масштабе), f – частота (1/год, в логарифмическом масштабе). Сплошные линии – спектры по данным палеореконструкций (см. табл. 1). Точечным красным и штриховым голубым пунктиром (две ветви в низкочастотном диапазоне) показана обобщенная линия, составленная из отрезков с указанным значением коэффициента k = 2, 0.6, 2, 1.67 (см. табл. 1). Годовой цикл отфильтрован. Fig. 3. Spectra of temperature fluctuations (in relative units) according to paleoreconstruction data (see tabl. 1) and a generalized line composed of segments with the specified value of the coefficient k = 2, 0.6, 2, 1.67, and in the low-frequency range it has two branches. The annual cycle is filtered out.

Таблица 1. Показатели степени (k) по различным данным Table 1. Exponents (k) for various data

Утверждение факта множественности колебаний требует расшифровки. Во-первых, их следы можно реально обнаружить в результатах палеореконструкций, которые представлены рядами сложной структуры с обилием вариаций различной амплитуды, частоты и фазы, появляющимися и исчезающими аномалиями разной продолжительности и выраженности. Во-вторых, их реальность связана именно с тем фактом, что спектры непрерывны, т.е. для каждой частоты существует колебание с определенной амплитудой (энергией).

На рис. 3 показаны примеры спектров, охватывающие разные диапазоны изменчивости. Отметим, что эти результаты совершенно не похожи на те, что представлены в (Mitchell, 1976) и несколько десятков лет использовались как основа понимания закономерностей климатической изменчивости. Набор спектров позволяет провести обобщающую линию, собранную из отрезков со специфическими значениями $k$ . Их выбор связан не просто с формальным усреднением результатов, поскольку малопродуктивно искать “точные” величины $k$ в случае небольшой выборки. В данном случае для аппроксимации $k$ подбираются натуральные числа, поскольку в этом случае форма спектра может быть описана из соображений размерностей физических величин.

Поведение обобщающей линии в высокочастотном диапазоне близко к закону (1) с $k=–2$, а в низкочастотной области проведены две ветви с k = 1.67 ≈ –5/3 и k = –2. Эти значения дают основания предполагать, что поведение климатической изменчивости определяется колмогоровским каскадным процессом ( k = –5/3) и броуновским движением ( k = –2). В промежуточной области “вековых” колебаний климата величина существенно меньше (–0.6), что подчеркивает то, что формирование климатической изменчивости имеет разный генезис на разных частотах.

Ситуации, когда $k$ выражено вещественным числом, могут быть исправлены (если это представляется возможным) включением в множитель формулы (1) функции вида $f\text{'}$ с показателем степени, дополняющим k до рационального числа (Голицин, 2013). В случае, когда это сделать нельзя, используется также физически реальное так называемое фрактальное броуновское движение (Кроновер, 1999; Lovejoy, 2022).

Колмогоровский спектр временных микропульсаций температуры описывается формулой

$S~{\epsilon }_T{f}^{-5/3}{\left(\frac{v}{\epsilon }\right)}^{1/6}$, (2)

где ${\epsilon }_T$ – диссипация неоднородностей температуры, имеющая размерность К ²/с, ν – кинематическая вязкость и ε – диссипация кинетической энергии. Эта строго обоснованная зависимость (Лазерное …, 1976) основана на предположении, что поле температуры изначально обладает определенной неоднородностью (“энергией”). При турбулентном движении в процессе каскадного дробления вихрей поле температуры будет становиться все более и более пестрым, но стока “энергии” нет, она сохраняется до самых малых масштабов, когда, наконец, становится эффективной молекулярная теплопроводность, выравнивающая температуру. Отметим, что поскольку каскадный перенос задается механикой турбулентного движения, в формуле (2) присутствуют определяющие его параметры – ν и ε. Однако они играют, как видно, в значительной степени фоновую роль, из-за того, что входят в формулу (2) с маленьким показателем степени.

Применительно к климатической изменчивости, формула (2) привлекательна следующими обстоятельствами. Во-первых, как только что отмечено, она аппроксимирует спектральное распределение эмпирических данных. Во-вторых, в нее входит ${\epsilon }_T$, поэтому она характеризует именно передачу энергии от области накачки (происходящей в диапазоне частот, отвечающих циклам Миланковича) в сторону высоких частот. Использование какой-либо другой закономерности (например, не –5/3, а –4/3) возможно с точки зрения точности аппроксимации эмпирических данных, но этот закон не ответственен за перенос энергии.

С другой стороны, трудность интерпретации формулы (2) в том, что у нее должно быть совершенно другое (не микромасштабное) физическое наполнение. Это касается понимания механизмов реализации каскадного процесса и выравнивания температуры. Так, в работе (Huybers, Curry, 2006) предполагается, без каких-либо объяснений, что каскад обеспечивают нелинейные процессы динамики ледниковых щитов. Это использование общей идеи о том, что энергетическое взаимодействие между модами изменчивости возможно только в нелинейной системе, и упомянутые авторы взяли адекватный по временным масштабам динамический процесс. Тогда разумно искать механизмы и в других нелинейных климатоформирующих процессах, связанных, например, с взаимодействием климатической системы с геобиохимическим циклом углерода, с взаимодействием ледниковых щитов с астеносферой, и др. В качестве механизма выравнивания температуры следует рассматривать, возможно, процесс макротурбулентной теплопроводности, обусловленный переносом тепла в атмосфере и океане. Однако все это спекулятивные рассуждения, не подкрепленные какими-либо конкретными исследованиями. Поэтому пока что предлагается просто принять формулу (1) с показателем степени 5/3, позволившую из разумных соображений охарактеризовать особенности спектра изменчивости температуры.

В области низких частот выделена и вторая ветвь функции спектральной плотности, характеризуемая поведением с k = 2 (рис. 3). Спектры такого рода характеризуют случайный процесс, называемый красным шумом (в отличие от белого шума, признаком которого является постоянство спектра). Такое же поведение характерно для изменчивости высоких частот – на многомесячном – межгодовом масштабах. Данному эмпирическому результату вновь можно поставить в соответствие теоретическую модель, выраженную стохастическим уравнением Ланжевена. В нем рассматривается динамика глобально усредненной температуры воздуха, вариация которой определяется планетарным радиационным теплообменом (с характерным временем изменений ${\lambda }^{-1}$ , где λ составлен из параметров климатической системы) и быстрыми флуктуациями (с масштабом $\tau \ll {\lambda }^{-1}$) перераспределения тепла внутри климатической системы. Решение, построенное для функции спектральной плотности, имеет вид (Hasselmann, 1976; Демченко, Кислов, 2010):

При условии, что ${\lambda }^2\ll f^2$ получается закон, обозначавшийся выше как k = 2, а множитель оказывается равен $b=2\tau {\sigma }^2$ (Hasselmann, 1976), где ${\sigma }^2$ – дисперсия быстрых флуктуаций К²/с², причем размерность величины b есть К²/с, т.е. это диссипация флуктуаций температуры.

Данная математическая теория описывает эволюцию динамической системы, в которую включены элементы, обладающие принципиально различной инерционностью. Быстрые разнознаковые вариации теплообмена не полностью погашают друг друга, в результате их влияние накапливается, формируя долгоживущую аномалию определенного знака. Например, быстрые атмосферные воздействия (на масштабах в несколько суток) посредством возмущения потоков тепла формируют долгоживущие аномалии температуры Мирового океана (Hasselmann, 1976; Hall, Manabe, 1997; Dommenget, Latif, 2002; Демченко, Кислов, 2010). Отражением этого механизма является ветвь обобщенной кривой в высокочастотной области рис. 3.

Применительно к низкочастотной области рис. 3 переменные, входящие в формулу (3), имеют тот же смысл, но в рассматриваемом диапазоне иные элементы климатической системы создают быстрые и медленные флуктуации. Учитывая характерные масштабы инерционности, можно считать, что медленные изменения климата ассоциируются с эволюцией глобального оледенения, активизируемой согласованной статистикой потоков тепла и влаги, и аномалиями углеродного цикла.

Если с точки зрения формальной статистики подобранный показатель степени не равен –2, то поведение будет описываться, как уже было отмечено, фрактальным броуновским движением. Его аналитическое обоснование более сложно. Один из реализованных путей связан с усложнением модели Будыко–Селлерса за счет введения эффекта, согласно которому поток тепла через поверхности раздела океана и атмосферы пропорционален половинной (не первой) производной температуры поверхности. При этом итоговое выражение превращается в дифференциальное уравнение с дробной производной (Lovejoy, 2020). Этим достигается то, что связь с температурой не является мгновенной, а зависит от всей предыдущей истории воздействия, и из-за этого у системы появляются специфические свойства.

Другой путь предложен П.Ф. Демченко: степень k в формуле (1) может быть эффективно уменьшена, если рассматривать не простой “разгон” инерционной системы быстрыми флуктуациями, а принять во внимание эффекты обратной связи, когда при формировании “медленной” изменчивости определенным способом меняются и свойства быстрых флуктуаций (Демченко, Кислов, 2010).

Третий путь – искать интерпретацию с позиций других законов. Так, близкий показатель степени k = 11/5 есть спектр Обухова–Больджано, объясняющий вариации, вызванные эффектами плавучести, и в условиях неточной информации его также используют при анализе вариаций климата (Lovejoy, 2019).

В целесообразности “улучшения” законов –5/3 и –2 есть большие сомнения. Как уже отмечено, “точные” значения $k$  малонадежны, поэтому делать упор на отклонениях нет оснований. Кроме этого, неэффективно применять сложные теоретические конструкции в заведомо простых, упрощенных схемах глобального теплообмена, из которых априорно исключены многие важнейшие механизмы. Представляется оправданным рассматривать упрощенные подходы лишь как демонстрацию возможности тех или иных эффектов, а их более детальную реализацию искать уже в полных моделях Земной системы.

Обратимся к масштабу вековых колебаний. Здесь показатель степени в формуле (1) невелик (рис. 3). По-видимому, тут колмогоровский каскадный перенос энергии от интервала циклов Миланковича уже начинает затухать. И закон красного шума (высокочастотной области) перестает работать в диапазоне ${\lambda }^2\gg f^2$ (см. формулу (3)). В контексте проведенного выше анализа, интерпретация такого “побеления” спектра связана с тем, что энергия для активизации “вековых” изменений климата “долетает” сюда с двух сторон – из зоны тысячелетних колебаний и из межгодовой области (Huybers, Curry, 2006). Кроме этого, события данного масштаба возникают в ответ на соответствующие радиационные форсинги (см. выше).

В континууме “вековых” вариаций климата особняком стоят события DO и Н, у которых механизм формирования связан с процессами Северной Атлантики, причем и для них определенная связь с низкочастотными событиями прослеживается. Так, обращено внимание на то, что события DO и Н и связанные с ними интерстадиалы и стадиалы Гренландии структурированы в форме так называемых циклов Бонда (Rousseau et al., 2022). Эти циклы были максимально выражены тогда, когда ледяные щиты Северного полушария достигли максимальной протяженности и объема. Поскольку их нарастание и убывание в течение четвертичного периода зависят от параметров планеты, делается вывод, что с ними косвенно связаны резкие изменения климата (Rousseau et al., 2022). Однако и здесь скорее описывается эффект группировки явлений, а не физика разномасштабного взаимодействия.

ЗАКЛЮЧЕНИЕ

Суммируем кратко полученные результаты.

Общее похолодание плиоцена и плейстоцена обусловлено монотонным снижением концентрации СО ₂ в кайнозойской эре. В плиоцене чувствительным элементом климатической системы, усваивающим внешние воздействия, была муссонная система Северного полушария. Изменение фоновой температуры создало предпосылки появления оледенений, а также перестройку во второй половине плейстоцена преимущественной ритмичности климата от 41 к 100 тыс. л. с увеличением амплитуды колебаний. Механизм возникновения 100-тысячелетних климатических ритмов можно объяснить за счет стохастического резонанса внутренней изменчивости и вариаций эксцентриситета.

Регулярные циклы Миланковича с периодичностями 41, 23 и 19 тыс. л. (связанные с углом наклона земной оси и вариациями положения планеты на орбите) проявляются во второй половине плейстоцена в колебаниях климата на фоне шума. Он активизируется поступлением энергии как от энергонесущего диапазона, так и из диапазона высоких частот.

Изменения климата в диапазоне “вековых” масштабов связаны с поступлением энергии с двух сторон, со стороны медленных и быстрых процессов. В первом случае это перенос со стороны энергонесущих циклов Миланковича, во втором – накачка со стороны высоких частот. Поэтому эти вариации, в определенном смысле, наиболее сложны для причинно-следственного анализа. Кроме того, в этот диапазон входят колебания климата, представляющие собой реакцию на внешние радиационные форсинги, а также вариации Дансгора-Оешгера и Хайнриха, имеющие характер специфической океанически-ледниковой природы.